Статически неопределимые задачи на кручение

При кручении, так же как и при растяжении, встречаются задачи, решение которых не может быть получено с помощью одних только уравнений равновесия. Число неизвестных в таких задачах превышает число уравнений равновесия. Порядок решения таких задач тот же самый, что и при решении статически неопределимых задач на растяжение - сжатие.

брус стержень деформация кручение

Отсюда определяем TA и подставляем в для определения TB

Кручение тонкостенного бруса замкнутого профиля.

Значительно более жесткими и поэтому более целесообразными при кручении являются тонкостенные стержни замкнутого профиля.

Рассмотрим цилиндрический стержень, поперечное сечение которого имеет достаточно общую форму.

t - меняется достаточно медленно

Геометрическое место точек, равноотстоящих от внешнего и внутреннего контуров поперечного сечения, называются средней линией сечения.

Возникающие при кручении касательные напряжения постоянны по толщине и направлены по касательной к средней линии.

Произведение касательного напряжения на толщину есть величина, постоянная для всех точек средней линии сечения.

Спроецируем все силы на направление оси стержня.

На внешней поверхности нагрузки отсутствуют, и следовательно, по закону парности касательных напряжений.

2. Касательные напряжения во внешних углах обращаются в нуль.

Парные касательных напряжений, действующие на внешней поверхности должны быть равны нулю. Следовательно, и

Решение, полученное методами теории упругости, для бруса прямоугольного сечения имеет следующую эпюру

Стержни, работающие на кручение за пределами упругости

Конструкция потеряет несущую способность при кручении в том случае, когда сечения первого и второго участков будут полностью охвачены пластическими деформациями.

Т.е. Т1 = Т1u Т2 = Т2u

Из условий равновесия Тu = T1u + T2u

Для определения T1u и T2u рассмотрим конкретные формы поперечного сечения

Круглое сечение

Кольцевое сечение

Тонкостенное сечение ()

площадь, ограниченная средней линией контура

Квадратное сечение

См. песочная аналогия

где V - объём поверхности постоянного ската с углом 450

Примечание: При нескольких внешних моментах необходимо рассмотреть несколько кинематически возможных состояний.

Свяжем Т с касательными напряжениями.

Элементарный момент относительно точки О.

где интегрирование распространяется на всю длину контура s.

Определить наибольшее напряжение в трубчатом стержне, если Т=1500 Н.м

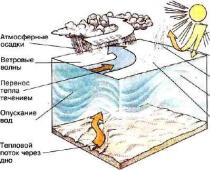
Мембранная аналогия при кручении

Задача о кручении бруса сводится к тому же дифференциальному уравнению, что и задача о равновесии пленки, натянутой на контур того же очертания и нагруженной равномерно распределенным давлением.

Аналогом напряжения является угол, который составляет касательная к поверхности пленки с поверхностного контура.

Т - Аналогом крутящего момента является объем, заключенный между плоскостью контура и поверхностью пленки.

Характер деформации пленки под действием давления можно представить хотя бы ориентировочно. Таким образом, всегда имеется возможность представить и закон распределения напряжений при кручении бруса с заданной формой сечения.

При помощи мембранной аналогии можно получить не только качественные, но и колличественнные соотношения. Для этого используется не сложный прибор, который замеряет прогибы с помощью микрометра. Использование гидростатического давления жидкости для нагружения мембраны позволяет определить крутящий момент по объему жидкости между мембраной и плоскостью. Для тарировки приборов такого типа могут быть использованы простейшие поперечные сечения, для некоторых известны аналитические решения.

При расчете на кручение прямых брусьев, жестко защемленных одним концом, а также при расчете валов (представляющих собой вращающиеся брусья, нагруженные взаимно уравновешенными скручивающими моментами) значения крутящих моментов в поперечных сечениях можно определить с помощью одних лишь уравнений равновесия (методом сечений). Следовательно, такие задачи являются статически определимыми.

Задачи расчета на кручение являются статически неопределимыми, если крутящие моменты, возникающие в поперечных сечениях скручиваемых стержней, нельзя определить с помощью только уравнений равновесия. Для решения этих задач дополнительно к уравнениям равновесия, составляемым для системы в целом или ее отсеченной части, необходимо составить также уравнения перемещений, основанные на рассмотрении характера деформации системы.

Рассмотрим для примера брус круглого сечения, жестко заделанный обоими концами и нагруженный моментом ЗЛ на расстоянии а от левого конца (рис. 23.6, а).

Для решения данной задачи можно составить лишь одно уравнение равновесия - в виде равенства нулю суммы моментов относительно оси бруса:

где и - реактивные скручивающие моменты, возникающие в заделках.

Дополнительное уравнение для решения рассматриваемой задачи можно получить следующим образом. Отбросим левое опорное закрепление бруса, но оставим правое (рис. 23.6, б).

Поворот левого конца полученного таким путем бруса должен быть равен нулю, т. е. так как в действительности этот конец жестко закреплен и не может поворачиваться.

На основании принципа независимости действия сил уравнение перемещений имеет вид

Здесь - угол поворота левого конца бруса от действия внешнего скручивающего момента (рис. 23.6, в); - угол поворота левого конца от действия внешнего момента (рис. 23.6, г).

По второй из формул (14.6), учитывая, что правый конец бруса не поворачивается (т. е. ), и по формуле (13.6) находим

Подставим эти значения в уравнение перемещений:

Из уравнения равновесия

После определения моментов и эпюру крутящих моментов можно построить обычным способом, т. е. как для статически определимого бруса (рис. 23.6, д). Для рассмотренной задачи эта эпюра представлена на рис. 23.6, е.

Наглядное представление об изменении углов поворота поперечных сечений бруса по его длине дает эпюра углов поворота (иногда ее называют эпюрой углов закручивания). Каждая ордината этой эпюры дает в принятом масштабе величину угла поворота соответствующего поперечного сечения бруса.

Построим такую эпюру для бруса по рис. 23.6, д, учитывая при этом, что значение уже найдено и эпюра крутящих моментов построена (см. рис. 23.6, е). Крайнее правое сечение А бруса неподвижно, т. е. Произвольное поперечное сечение, принадлежащее участку АС и отстоящее на расстояние от правого конца, повернется на угол [см. вторую из формул (14.6)]

Здесь - угол закручивания на участке длиной определяемый по формуле (13.6).

Таким образом, углы поворота изменяются по линейному закону в зависимости от расстояния Подставляя в полученное выражение найдем угол поворота сечения С:

Заметим, что всегда при нагружении бруса постоянного сечения сосредоточенными скручивающими моментами эпюра углов поворота поперечных сечений на каждом из участков бруса линейна.

Для построения эпюры на участке СВ вычислим угол поворота сечения В. На основании второй из формул (14.6) и формулы (13.6)

Этот результат подтверждает правильность решения задачи, так как по условию сечение В заделано жестко. Таким образом, кроме чисто иллюстративного значения, построение эпюры углов поворота поперечных сечений можно рассматривать как метод контроля решения некоторых статически неопределимых задач.

Построенная по полученным значениям эпюра углов поворота представлена на рис. 23.6, ж.

При действии на брус нескольких внешних скручивающих моментов, а также для брусьев, имеющих на отдельных участках разные поперечные сечения, составление дополнительного уравнения производится способом, аналогичным показанному (см. пример 5.6).

При расчете цилиндрических пружин наряду со статически определимыми встречаются также и статически неопределимые задачи.

Если концы пружины не закреплены и могут свободно перемещаться вдоль оси пружины или если закреплен лишь один ее конец, то задача расчета такой пружины статически определима. Если же оба конца пружины неподвижно закреплены, то задача ее расчета статически неопределима. Для ее решения необходимо составить дополнительное уравнение перемещений. Составление этого уравнения аналогично составлению уравнения, применяемого при решении задач расчета прямого стержня, закрепленного обоими концами, на внешние нагрузки, действующие вдоль его оси. Составление дополнительных уравнений для такого типа задач рассмотрено выше в § 9.2 (см. также пример 3.6).

4.4. Статически неопределимые задачи кручения

Такие задачи обычно возникают, если перемещение вала ограничено в некоторых сечениях, например, (рис. 4.9), когда его концы защемлены. В

одно уравнение равновесия: :

входят два неизвестных момента в опорах, поэтому задача является статически неопределимой. Для ее решения составим дополнительное уравнение перемещений. Рассмотрим перемещения (углы поворота) сечений, являющихся границами участков вала..gif" width="99" height="27 src=">.

https://pandia.ru/text/78/579/images/image007_54.gif" width="99 height=26" height="26">.

Так как сечение вала защемлено, то , откуда: https://pandia.ru/text/78/579/images/image011_42.gif" align="left" width="258" height="186">

Потенциальная деформация деформации участка вала длиной dz будет:
Так как при кручении τ = (МК / IР) r, то

Сокращая на IР, получим выражение для потенциальной энергии деформации при кручении

4.6 . Кручение стержней некруглого поперечного сечения

https://pandia.ru/text/78/579/images/image018_20.gif" align="left" width="324" height="237 src="> При кручении стержней (валов) не круглого и не - кольцевого поперечных сечений, не выполняются допущения, принятые при кручении круглых и кольцевых валов: плоские поперечные сечения стержня не остаются плоскими при кручении, а депланируют (искривляются); прямые радиусы, проведенные в плоских сечениях, искривляются; рассто-яние между сечениями изменяется (рис. 4Если стержень постоянного сечения по всей длине негде не защемлен и закручивающие моменты, расположены на его концах, то все сечения депланируют одинаково, и нормальные напряжения не возникают. Такое кручение называется свободным. Однако, с достаточной для практических целей точностью, для некруглых стержней можно пользоваться формулами, выведенными для круглого стержня, заменив и https://pandia.ru/text/78/579/images/image021_17.gif" width="23" height="27 src=">- момент инерции при кручении, и -момент сопротивления при кручении.

https://pandia.ru/text/78/579/images/image024_18.gif" width="90" height="49">, ,

Для прямоугольного поперечного сечения (рис. 4.12)

https://pandia.ru/text/78/579/images/image027_17.gif" width="87" height="29 src=">.

Здесь и - зависят от отношения .

Коэффиценты.	Отношение большей стороны сечения к меньшей .

Дифференциал" href="/text/category/differentcial/" rel="bookmark">дифференциальному уравнению, что и задача о равновесии тонкой пленки, натянутой на контур того же очертания, что и контур поперечного сечения стержня и нагруженной равномерно распределенным давлением. Аналогом напряжения является угол, который составляет касательная к поверхности пленки с плоскостью контура, а аналогом крутящего момента - объем, заключенный между плоскостью контура и поверхностью пленки. На рис. 4.13,а показано поведение пленки под давлением, на рис. 4.13,б приведено качественное распределение напряжений при кручении стержня сложного профиля. С помощью специального прибора и тарированной пленки можно получить и количественные результаты. Для этого, чтобы учесть жесткость пленки, такой же эксперимент проводят с круглым отверстием, откуда и получают необходимую жесткость пленки, так как решение в этом случае можно получить точно.

4.7. Свободное кручение тонкостенных стержней

Тонкостенными называют стержни, у которых один размер поперечного сечения - толщина профиля , меньше другого - длины контура поперечного сечения s. Стержни бывают открытого (рис. 4.14) и замкнутого (рис. 4.15) профилей. Используем мембранную аналогию. Характер поведения пленки и, соответственно, касательных напряжений в тонкостенных стержнях открытого и замкнутого профилей принципиально разный (рис. 4.16 и рис. 4Если стержень открытого профиля выпрямить в длинный прямоугольник, то форма пленки не изменится.

Тогда для прямоугольного сечения при , имеем: ,..gif" width="22" height="25"> прямоугольников, то

..gif" width="42" height="26">.

Рассмотрим расчет статически неопределимой системы на кручение на конкретном примере.

Пример . Определить из расчета на прочность при допускаемое значение скручивающего момента для вала, жестко защемленного обоими концами и нагруженного, как показано на рис. 10.8, а.

Рис. 10.8. Схема статически неопределимого вала

В заделках возникают реактивные моменты m A и m B (рис. 10.8, а). Составим уравнение равновесия относительно продольной оси вала:

Таким образом, задача является один раз статически неопределимой – одно уравнение статики и два неизвестных реактивных момента. Для составления уравнения перемещений отбросим правую заделку, заменив ее действие на вал неизвестным реактивным моментом . Полученная таким образом статически определимая система (рис. 10.8, б) эквивалентна заданной, и, следовательно, угол поворота сечения B равен нулю:

Применяя принцип независимости действия сил, запишем уравнение перемещений для сечения B в виде

При действии только момента m 1 угол поворота сечения В равен углу закручивания участка АС , т. е.

Аналогично при действии только момента m 2:

При действии только момента m B = X имеем:

Для упрощения вычислений выразим

Подставляя значения углов поворота в уравнение совместности деформаций и учитывая последнее равенство, получаем:

Подставляя значение Х в уравнение равновесия, найдем:

После раскрытия статической неопределимости эпюры крутящих моментов, касательных напряжений и углов закручивания строятся обычным способом. Эта эпюры представлена на рис. 10.8, в, г, д.

Опасными являются сечения участка ВЕ . Следует отметить, что сечения, в которых возникают наибольшие крутящие моменты (участок АС ), в данном случае менее опасны.

Запишем условие прочности:

Расчет цилиндрических винтовых пружин

С малым шагом витков

Во многих механизмах и машинах, например в рессорах вагонов и автомобилей, применяют винтовые пружины. Эти пружины навивают из проволоки круглого поперечного сечения, изготовленной из специальных марок стали. При проектировании таких пружин необходимо уметь вычислять наибольшие напряжения (для проверки на прочность) и определять деформацию пружины (ее удлинение или прогиб). Точный расчет винтовых пружин достаточно сложен, так как материал пружины испытывает одновременно кручение, сдвиг, изгиб и растяжение.

Пружина с малым шагом витков – это такая пружина, у которой угол между плоскостью, перпендикулярной к оси пружины, и плоскостью витка не превышает 14º.

Пусть винтовая пружина растягивается (или сжимается) силами F , имеет средний диаметр D = 2R и изготовлена из проволоки диаметром d (рис. 10.9, а). Для определения внутренних усилий в пружине применим метод сечений.

Рис. 10.9. Схема винтовой пружины с малым шагом витков

Верхняя часть пружины (рис. 10.9, б) будет находиться в равновесии под действием внешней силы F и внутренних усилий в проведенном сечении прутка, которые можно представить суммой силы F и крутящего момента М кр .

Считая, что угол наклона витка , можно пренебречь остальными силовыми факторами (продольной силой и изгибающим моментом). Материал пружины испытывает срез и кручение.

Сила вызывает в поперечном сечении касательные напряжения , которые определяются по формуле

Считаем, что касательные напряжения распределяются по сечению равномерно (рис. 10.9, г).

Максимальные касательные напряжения от кручения равны:

Распределение касательных напряжений от кручения показано на рис. 10.9, в.

Опасной точкой на контуре сечения является точка А , в которой направления касательных напряжений совпадают. Таким образом, максимальные касательные напряжения равны:

Так как и на практике то часто действием пренебрегают.

Условие прочности для пружин малой кривизны (приближенный расчет):

Условие прочности для пружин малой кривизны:

Из формул для определения следует, что увеличение диаметра пружины D уменьшает ее прочность, а увеличение диаметра проволоки d – увеличивает.

При определении деформации пружины будем учитывать только кручение витков.

Изменение длины пружины вдоль оси под действием внешней нагрузки называется осадкой пружины λ

где n – число витков;

G – модуль сдвига.

Зависимость осадки λ от осевой нагрузки F называется характеристикой пружины. Обычные пружины имеют линейную характеристику.

Усилие F , при котором перемещение λ равно единице (1 м), называется жесткостью пружины с , которая определяется по формуле

размерность жесткости кН/м.

Итак, увеличение числа витков n и диаметра пружины D уменьшает жесткость пружины, а увеличение диаметра проволоки d повышает жесткость пружины.

Пример расчета

Задача 1. Для заданной схемы (рис. 10.10, а) определить значение m и построить эпюру крутящих моментов.

Решение.

1. Методом сечений на каждом участке вала определяем значение крутящего момента.

Рис. 10.10. Схема вала для построения эпюры

крутящих моментов

1-й участок . Рассмотрим равновесие левой отсеченной части вала. Составим уравнение равновесия:

На 1-м участке имеет отрицательное значение, так как со стороны внешней нормали к отсеченной части вращается по часовой стрелке.

2-й участок:

3-й участок:

с другой стороны:

2. Эпюра с учетом знаков построена на рис. 10.10, б.

Задача 2. Вал круглого поперечного сечения диаметром d = 40 мм скручивается моментами m 1 = 0,6 кНм, m 2 = 1,2 кНм и m 3 = 0,8 кНм (рис. 10.11, а). Проверить прочность вала и определить абсолютный угол закручивания концевого сечения, если [τ ] = 80 МПа, G = = 8×10 4 МПа.

Рис. 10.11. Схема вала круглого поперечного сечения

Решение.

1. Методом сечений строим эпюру крутящих моментов (рис. 10.11, б).

2. Определим геометрические характеристики поперечного сечения вала:

3. Проверяем прочность вала:

4. Определяем абсолютный угол закручивания концевого сечения:

Задача 3. Построить эпюру углов закручивания для ступенчатого стального вала, нагруженного, как показано на рис. 10.12, а. G = = 8×10 4 МПа.

Решение.

1. Определим геометрические характеристики сечений каждой ступени вала:

Рис. 10.12. Схема ступенчатого вала

2. Построим эпюру крутящих моментов (рис. 10.12, б).

3. Определим углы закручивания в характерных сечениях вала по формуле

Изображена на рис. 10.12, в.

Задача 4. Определить внутренний и наружный диаметры полого стального вала, передающего мощность N = 100 кВт и вращающегося с угловой скоростью ω = 80 рад/с, если [τ ] = 60 МПа; α = d /D = 0,6, [θ ] = 45×10 –4 рад/м, G = 8×10 4 МПа.

Решение.

1. Определим крутящий момент на валу:

2. Из условия прочности определим момент сопротивления сечения вала:

3. Определим наружный диаметр вала из условия жесткости:

4. Принимаем D = 80 мм, d = 48 мм.

Задача 5. Вал диаметром 90 мм передает мощность N = 80 кВт. Определить предельное число оборотов вала, если [τ ] = 60 МПа.

Решение.

1. Определим момент сопротивления поперечного сечения вала:

2. Из условия прочности определим крутящий момент на валу:

3. Определим предельное число оборотов вала:

Задача 6. Какую мощность может передать вал, вращающийся с угловой мощностью ω = 20 рад/с, диаметром d = 100 мм при допускаемом напряжении [τ ] = 60 МПа и допускаемом угле закручивания
[θ ] = 45 × 10 –4 рад/м. Модуль сдвига G = 8 × 10 4 МПа.

Решение .

1. Определим геометрические характеристики поперечного сечения вала:

2. Передаваемая валом мощность определяется по формуле

3. Из условия прочности имеем:

Из условия жесткости:

Принимаем

Задача 7. d = 6 мм, имеет n = 10 витков. Диаметр пружины D = 66 мм. Пружина растягивается осевыми силами F = 300 Н. Проверить прочность пружины, если [τ ] = 240 МПа. Определить удлинение и жесткость пружины и накапливаемую потенциальную энергию.
G = 8 × 10 4 МПа.

Решение.

1. Определим поправочный коэффициент:

2. Определим касательные напряжения, возникающие в поперечных сечениях прутка пружины:

3. Определим удлинение пружины под действием внешней нагрузки:

4. Определим жесткость пружины:

5. Определим потенциальную энергию деформации:

Задача 8. Стальная цилиндрическая пружина сжимается осевыми силами F (рис. 10.13). Пружина навита из проволоки диаметром d = 5 мм, с шагом t = 10 мм и имеет диаметр D = 30 мм. Определить значение сил F , при которых будет достигнута ее предельная осадка. G = 8 × 10 4 МПа.

Рис. 10.13. Схема пружины, сжатой осевыми силами

Решение.

1. Запишем условие жесткости пружины при сжатии:

2. Определим предельное значение сил F :

10.7. Задачи для самостоятельного решения

Задача 9. Для заданной схемы нагружения вала (рис. 10.14) построить эпюру крутящих моментов.

Рис. 10.14. Схема вала для построения эпюры крутящих моментов

Задача 10. Для заданного ступенчатого вала (рис. 10.15) построить эпюру крутящих моментов.

Рис. 10.15. Схема ступенчатого вала для построения эпюры

крутящих моментов

Задача 11. К валу постоянного сечения диаметром d = 50 мм (рис. 10.16) приложены моменты m 1 = 1 кНм, m 2 = 0,2 кНм, m 3 = 0,4 кНм и m 4 = 0,4 кНм. Проверить прочность вала, если [τ ] = 60 МПа. Определить полный угол закручивания, если G = 8 × 10 4 МПа.

Рис. 10.16. Схема вала постоянного сечения

Задача 12. Цилиндрическая пружина, изготовленная из стальной проволоки диаметром d = 5 мм, растягивается силами F = 400 Н. Диаметр пружины D = 30 мм. Проверить прочность пружины, если [τ ] = 500 МПа. Определить число витков пружины, при котором она удлиняется на 40 мм. G = 8 × 10 4 МПа.

Задача 13. Определить требуемый диаметр проволоки винтовой цилиндрической пружины для осевой нагрузки F = 1,2 кН, если D /d = 6 и [τ ] = 500 МПа.

Задача 14. Для заданной схемы нагружения (рис. 10.17) определить диаметры проволоки для обеих пружин, если D 1 /d 1 = D 2 /d 2 = 8 и [τ ] = = 600 МПа.

Рис. 10.17. Схема бруса, подвешенного на двух пружинах

10.8. Контрольные вопросы

1. Какой вид нагружения называется кручением?

2. Что называется валом? Что такое крутящий момент?

3. Какие деформации возникают при кручении?

4. Какие внутренние силовые факторы возникают при кручении?

5. Вывести формулу для определения напряжений в поперечном сечении скручиваемого круглого вала.

6. Вывести формулы для определения относительного и полного углов закручивания круглого вала.

7. Что такое эпюра крутящего момента и как она строится?

8. Как распределяется касательное напряжение при кручении? Чему равно напряжение в центре круглого поперечного сечения?

9. Написать формулу для расчета напряжения на поверхности вала при кручении. Как изменится напряжение, если диаметр вала увеличится в два раза?

10. В чем заключается расчет на прочность при кручении?

11. В чем заключается расчет на жесткость при кручении?

12. Почему при одинаковой прочности и жесткости вал кольцевого поперечного сечения легче, чем вал сплошного круглого сечения?

13. Как вычислить потенциальную энергию деформации, накапливаемую валом при кручении?

14. Расчет статически неопределимых валов.

15. Расчет цилиндрических пружин с малым шагом витков. Что такое осадка и жесткость пружины, как они определяются?

Сложное сопротивление

В отличие от рассмотренных ранее круглых стержней, кручение стержней некруглой поперечной формы обладает особенностями. Основная из них – депланация . Это явление того, что сечения перестают быть плоскими, депланируют. Формулы, основанные на гипотезе плоских сечений, теряют силу. Возникают нормальные напряжения.

Различают свободное и стеснённое кручение. Свободным называют такое кручение, при котором депланация постоянна по длине стержня и её можно характеризовать величиной перемещения в осевом направлении. Кручение стержня, при котором депланация сечения по длине стержня изменяется, называется стеснённым кручением . В этом случае возникает особый вид внутреннего усилия – бимомент, влияющий на распределение нормальных и касательных напряжений по сечению.

Стержни с некруглым поперечным сечением могут быть различны (рис. 11.1).

Рис. 11.1. Стержни с некруглым поперечным сечением: а) толстостенные; б) тонкостенные замкнутого и открытого профиля

Толстостенными называют стержни, имеющие размеры различных элементов сечения соизмеримые с размерами самого сечения. Деформация толстостенных стержней имеет сложный характер, задачи о кручении таких стержней решаются аналитически или численно методами теории упругости.

Тонкостенными называют стержни, у которых длина контура поперечного сечения намного больше толщины сечения.

Расчёт тонкостенных стержней открытого и замкнутого профиля на стеснённое кручение изучается в теории тонкостенных стержней, разработанной проф. В.З. Власовым.

Решение задачи свободного кручения стержней некруглого поперечного сечения получено Сен-Венаном.

При кручении прямоугольного поперечного сечения наибольшее напряжение возникает посредине длинной стороны контура (рис. 11.2). Для его вычисления используют формулу (11.1).

Здесь W t =αhb 2 - момент сопротивления при кручении, α – коэффициент Сен-Венана, h и b размеры прямоугольного сечения (рис. 11.2).

Угол закручивания грузового участка длиной l c постоянным внутренним усилием находится по формуле (11.2)

Здесь I t =βhb 3 - момент инерции при кручении, β – коэффициент Сен-Венана.

Эп. τ[МПа]

Рис. 11.2. Эпюра касательных напряжений

Коэффициенты Сен-Венана α, β, γ определяются с помощью таблицы 11.1 в зависимости от отношения h/b .

Таблица 11.1

h/b
α	0,208	0,246	0,267	0,282	0,299	0,307	0,313	0,333
β	0,140	0,229	0,263	0,281	0,299	0,307	0,312	0,333
γ	1,000	0,795	0,753	0,745	0,743	0,742	0,742	0,742

Расчёт различных некруглых поперечных сечений на прочность и жёсткость выполняется аналогично изложенному в предыдущей лекции. С помощью условий прочности и жёсткости решаются задачи с целью подбора размеров поперечного сечения, определения допустимой нагрузки и проверки выполнения условий. В зависимости от профиля поперечного сечения по разному определяются геометрические характеристики поперечного сечения, фигурирующие в формулах для вычисления напряжений и перемещений. (Посмотреть эти формулы самостоятельно по учебнику).

Решение статически неопределимых задач при кручении . Задачи кручения стержней являются статически неопределимыми , если крутящие моменты, возникающие в поперечных сечениях стержня, не могут быть определены с помощью только одних уравнений равновесия. Для решения таких задач необходимо рассматривать деформированное состояние скручиваемого стержня. Алгоритм решения аналогичен изложенному в теме осевое растяжение–сжатие.

В случае постоянной жёсткости стержня удобно применять для решения статически неопределимых задач метод начальных параметров (ознакомиться с этим методом самостоятельно).

Задачи могут быть несколько раз статически неопределимыми. Рассмотрим один раз статически неопределимые задачи.

Рис. 11.3. Статически неопределимые стержни при кручении

а) Раскрытие статической неопределимости

∑ m X = 0; М А - М + М В n st

Перемещение (угол закручивания) точки В (жесткая заделка) невозможно, тогда это перемещение можно представить как сумму углов закручивания грузовых участков φ В = φ I + φ II = 0 (2).

М t =const можно представить в виде: (3). Подставим (3) в (2): . (4)

Запишем уравнения крутящих моментов на грузовых участках, рассматривая при этом равновесие правой части, содержащей опорную реакцию М В : М t ,I = М В - const, М t ,II = М В - М – const. При равенстве жесткостей на грузовых участках уравнение (4) примет вид:

М В

б) Раскрытие статической неопределимости

1. Рассмотрим статическую сторону задачи

Составим уравнение равновесия:

∑ m X = 0; М А + ml – М В = 0 (1), найдем степень статической неопределимости как разницу между неизвестными опорными реакциями и количеством уравнений статики n st = 2 – 1 = 1 – задача один раз статически неопределимая и для раскрытия статической неопределимости требуется еще одно уравнение.

2. Рассмотрим геометрическую сторону задачи

Перемещение (угол закручивания) точки В (жесткая заделка) невозможно, тогда это перемещение можно представить как сумму углов закручивания грузовых участков φ В = φ I = 0 (2).

3. Рассмотрим физическую сторону задачи

Угол закручивания на грузовом участке длиной, где М t описывается линейным уравнением можно представить в виде:

(3). Подставим (3) в (2): . (4)

Запишем уравнение крутящих моментов на грузовом участке, рассматривая при этом равновесие правой части, содержащей опорную реакцию М В : М t , I = - М В + mx , подставим уравнение внутреннего усилия в (4):

Решим полученное уравнение относительно одного неизвестного М В . Далее задача решается как статически определимая.

Расчёт стержней при кручении по предельному состоянию. Рассмотрим распределение касательных напряжений в поперечном сечении круглого стержня, выполненного из упругопластического материала, подчиняющегося идеализированной диаграмме Прандтля (рис. 11.4).

Рис. 11.4. Диаграмма Прандтля

τ max < τ s τ max = τ s . τ s τ s

M t = τ s W ρ Упругое ядро Пластический шарнир

(M t , lim )

Рис. 11.5. Распределение касательных напряжений в поперечном сечении

При углах сдвига γ ≤ γ s материал подчиняется закону Гука, т.е. τ = G γ, при γ = γ s касательное напряжение достигает предела текучести τ s , при γ > γ s материал «течёт» при постоянном напряжении τ = τ s . На этом заканчивается чисто упругая стадия работы (рис. 11.5 б) и момент достигает опасного значения. При дальнейшем увеличении крутящего момента эпюра напряжений приобретает вид, приведённый на рис. 11. 5 в. При увеличении крутящего момента упругое ядро уменьшается, и текучесть материала происходит по всему сечению, наступает состояние предельного равновесия, соответствующее максимуму несущей способности стержня. Для сплошного круглого сечения в случае, представленном на рис. 11. 5 г грузоподъёмность стержня повышается на 33% по сравнению с грузоподъёмностью, вычисленной для ситуации приведённой на рис. 11. 5 г.